lunes, 6 de mayo de 2013
Funciones Trigonométricas.
Obtén las medidas trigonométricas y el ángulo de los siguientes ángulos.
Obtén las medidas trigonométricas y el ángulo de los siguientes ángulos.
1- Obtener la hipotenusa.
C^2= a^2 + b^2
c^2= 3^2 + 2^2
c^2= 9 + 4
c^2= 13
c= raíz 13
c= 3.605
2. Obtener Seno, coseno y tangente de alfa.
Sen A = 3 = 0.8333
---
3.6
Cos A = 2 = 0.5555
---
3.6
tan A = 3 = 1.5
----
2
3. Se toma cualquier función trigonométrica y se obtienen los grados de A.
Sen A = 0.8333
A= sen -1 (0.8333)
A= 56.09°
Ejercicio 1.- Perímetro, Área y Volumen.
El perímetro de un polígono es la suma de la longitud de cada lado, si el polígono es regular, entonces el perímetro es igual al número de lados por la longitud de uno de ellos:
P = (n° de lados) (Longitud)
Si el perímetro de un triángulo equilátero es de 99 metros, ¿Cuánto mide cada lado?
P = ( n° l ) (longitud)
l = P / N° l
l = 99 / 3
l = 33 metros.
El área de una figura es la medida de la superficie y medir una superficie es determinar cuantas veces contiene a otra superficie conocida.
Un terreno de forma mide 35 m. y 45 m. en sus lados paralelos y el ancho mide 20 m. ¿Cuál es el área?
Formula del trapecio= (B + b) h
-------------
2
A= (45+35) 20
--------------
2
A= 1600
--------
2
A= 800 m^2
Volumen
Se almacenan granos en un cono que tiene 20 m de altura y un radio de 6 m. ¿Cuál es la capacidad de almacenamiento?
Formula del cono:

V = (3.1416 (6)^2) 20
-------------------------
3
V = (113.09) 20
--------------
3
V = 2261.946711
----------------
3
V = 753.98 m^3
El perímetro de un polígono es la suma de la longitud de cada lado, si el polígono es regular, entonces el perímetro es igual al número de lados por la longitud de uno de ellos:
P = (n° de lados) (Longitud)
Si el perímetro de un triángulo equilátero es de 99 metros, ¿Cuánto mide cada lado?
P = ( n° l ) (longitud)
l = P / N° l
l = 99 / 3
l = 33 metros.
El área de una figura es la medida de la superficie y medir una superficie es determinar cuantas veces contiene a otra superficie conocida.
Un terreno de forma mide 35 m. y 45 m. en sus lados paralelos y el ancho mide 20 m. ¿Cuál es el área?
Formula del trapecio= (B + b) h
-------------
2
A= (45+35) 20
--------------
2
A= 1600
--------
2
A= 800 m^2
Volumen
Se almacenan granos en un cono que tiene 20 m de altura y un radio de 6 m. ¿Cuál es la capacidad de almacenamiento?
Formula del cono:

V = (3.1416 (6)^2) 20
-------------------------
3
V = (113.09) 20
--------------
3
V = 2261.946711
----------------
3
V = 753.98 m^3
Ejercicio 5.- Teorema de Pitagoras.
La suma del cuadrado de los catetos es igual al cuadrado de la hipotenusa. Este teorema se utiliza solamente en los triángulos rectángulos.
Para verificar que un triángulo es rectángulo podemos aplicar también el teorema de Pitagoras.
Verifica si los triángulos son rectángulos.
a) 4, 7.5 y 8.5 b) 8, 15 y 12 c) 12, 15 y 20
8.5^2=4^2+7.5^2 15^2=8^2+12^2 20^2=12^2+15^2
72.25=16+56.25 223=64+144 400=144+225
72.25=72.25 223=208 400=369
Si es triángulo rectángulo No es triáng. rect. No es triáng. rect.
La suma del cuadrado de los catetos es igual al cuadrado de la hipotenusa. Este teorema se utiliza solamente en los triángulos rectángulos.
Para verificar que un triángulo es rectángulo podemos aplicar también el teorema de Pitagoras.
Verifica si los triángulos son rectángulos.
a) 4, 7.5 y 8.5 b) 8, 15 y 12 c) 12, 15 y 20
8.5^2=4^2+7.5^2 15^2=8^2+12^2 20^2=12^2+15^2
72.25=16+56.25 223=64+144 400=144+225
72.25=72.25 223=208 400=369
Si es triángulo rectángulo No es triáng. rect. No es triáng. rect.
Ejercicio 4.- Ángulos Internos de un polígono.
Los ángulos internos de un polígono se obtienen dividiendo ese polígono en triángulos para ver cuantos se forman internamente desde un vértice.
Fórmula:
 Ángulos internos= (Numero de lados-2) 180°
Ángulos internos= (Numero de lados-2) 180°
-Obtener la suma de los ángulos internos de los siguientes polígonos:
A) 38 lados
38-2= 36
(36) (180°)= 6480°
B) 10 lados
10-2= 8
(8) (180°)= 1440°
C) 17 lados
17-2= 15
(15) (180°)= 2700°
Los ángulos internos de un polígono se obtienen dividiendo ese polígono en triángulos para ver cuantos se forman internamente desde un vértice.
Fórmula:
 Ángulos internos= (Numero de lados-2) 180°
Ángulos internos= (Numero de lados-2) 180°-Obtener la suma de los ángulos internos de los siguientes polígonos:
A) 38 lados
38-2= 36
(36) (180°)= 6480°
B) 10 lados
10-2= 8
(8) (180°)= 1440°
C) 17 lados
17-2= 15
(15) (180°)= 2700°
Ejercicio 3.- Teoremas.
Si tenemos dos ángulos complementarios congruentes con otros dos, entonces el complemento de este también será congruente. Si tenemos dos ángulos suplementarios congruentes con otros dos, entonces el suplemento de este también será congruente.
En 2 rectas paralelas divididas por una transversal, uno de los ángulos mide 150°, calcula el valor de "x" y "y".
Si tenemos dos ángulos complementarios congruentes con otros dos, entonces el complemento de este también será congruente. Si tenemos dos ángulos suplementarios congruentes con otros dos, entonces el suplemento de este también será congruente.
En 2 rectas paralelas divididas por una transversal, uno de los ángulos mide 150°, calcula el valor de "x" y "y".
---- ---
AB || CD
x+ y= 150° 150°+ángulo "a"= 180°
-x+2y= 30° a= 30°
x+y= 150°
3y= 120
y= 120/3
y= 40°
x+40= 150°
x= 150-40
x= 110°
Ejercicio 2.- Semejanza de Triángulos.
Los triángulos son semejantes cuando tienen la misma forma aunque tengan diferente tamaño. Dos triángulos son semejantes si sus ángulos respectivos son congruentes, y sus lados homólogos y proporcionales.
Los triángulos son semejantes cuando tienen la misma forma aunque tengan diferente tamaño. Dos triángulos son semejantes si sus ángulos respectivos son congruentes, y sus lados homólogos y proporcionales.
Postulado: LAL
30/21 = 1.42
20/14= 1.42
Ángulo A= Ángulo E=90°
Ejercicio 1.- Triángulos congruentes.
Dos triángulos son congruentes si tienen el mismo tamaño y forma, de tal manera que si los superponemos uno con el otro, coinciden de manera exacta. Sabemos que la suma de los 3 ángulos internos de un triángulo es igual a 180° y también conocemos los 3 postulados de congruencia en los triángulos: ALA, LAL y LLL. Encuentra el valor de "x" y de "y" de las siguientes figuras, aplicando los postulados de congruencia.
Postulado: LAL
Triángulo Lado Ángulo
I I, X 60°
II I, X 3y
3y= 60°
y= 60
----
3
y= 20
Triángulo Lado Ángulo
I II, X 2X
II II, X 24
2x= 24°
x= 24
---
2
x= 12°
Dos triángulos son congruentes si tienen el mismo tamaño y forma, de tal manera que si los superponemos uno con el otro, coinciden de manera exacta. Sabemos que la suma de los 3 ángulos internos de un triángulo es igual a 180° y también conocemos los 3 postulados de congruencia en los triángulos: ALA, LAL y LLL. Encuentra el valor de "x" y de "y" de las siguientes figuras, aplicando los postulados de congruencia.
Postulado: LAL
Triángulo Lado Ángulo
I I, X 60°
II I, X 3y
3y= 60°
y= 60
----
3
y= 20
Triángulo Lado Ángulo
I II, X 2X
II II, X 24
2x= 24°
x= 24
---
2
x= 12°
Rectas y segmentos más importantes de un circulo.
CUERDA:
Una cuerda de una curva es un segmento de recta, cuyos extremos son dos puntos de la curva. La recta que contiene a una cuerda se denomina secante a la curva; si un extremo tiende al otro la recta límite se llama tangente a la curva.
 SECANTE:
SECANTE:
Es una recta que corta a una circunferencia en 2 puntos. Conforme estos puntos se acercan y su distancia se reduce a cero, la recta adquiere el nombre de recta tangente.
 TANGENTE:
TANGENTE:
La tangente a una curva en uno de sus puntos, es una recta que toca a la curva en el punto dado, el punto de tangencia(se puede decir que «forman un ángulo nulo» en la vecindad de dicho punto).
 RADIO:
RADIO:
Es la mitad del diámetro. Todos los radios de una figura geométrica poseen la misma longitud.
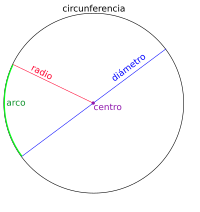
DIÁMETRO:
El diámetro es el segmento de recta que pasa por el centro y une dos puntos opuestos de una circunferencia, una superficie esférica o una curva cerrada.

CUERDA:
Una cuerda de una curva es un segmento de recta, cuyos extremos son dos puntos de la curva. La recta que contiene a una cuerda se denomina secante a la curva; si un extremo tiende al otro la recta límite se llama tangente a la curva.

Es una recta que corta a una circunferencia en 2 puntos. Conforme estos puntos se acercan y su distancia se reduce a cero, la recta adquiere el nombre de recta tangente.

La tangente a una curva en uno de sus puntos, es una recta que toca a la curva en el punto dado, el punto de tangencia(se puede decir que «forman un ángulo nulo» en la vecindad de dicho punto).

Es la mitad del diámetro. Todos los radios de una figura geométrica poseen la misma longitud.

DIÁMETRO:
El diámetro es el segmento de recta que pasa por el centro y une dos puntos opuestos de una circunferencia, una superficie esférica o una curva cerrada.

Ejercicio 8.- Construcción de un pentágono dentro de una circunferencia.
1.- Traza un diámetro (AB) y después una recta perpendicular (CD mediatriz).
2.- Traza el radio de uno de los puntos del diámetro (AB), de modo que corte la circunferencia (puntos E,F).
3.- Traza una recta con los puntos de corte (EF), de modo que intersecte el diámetro, el cual se nombrara el punto G
4.- Traza nuevamente el radio del circulo desde el punto "G", tienes que cortar el diámetro y a ese punto se le nombrara el punto "H".
5.- Abre el compás del punto "C" al punto "H" y realiza cortes a la circunferencia con esa medida, situándote como punto de inicio el punto C.
6.- Une los puntos de corte de la circunferencia que realizaste anteriormente (#5).

1.- Traza un diámetro (AB) y después una recta perpendicular (CD mediatriz).
2.- Traza el radio de uno de los puntos del diámetro (AB), de modo que corte la circunferencia (puntos E,F).
3.- Traza una recta con los puntos de corte (EF), de modo que intersecte el diámetro, el cual se nombrara el punto G
4.- Traza nuevamente el radio del circulo desde el punto "G", tienes que cortar el diámetro y a ese punto se le nombrara el punto "H".
5.- Abre el compás del punto "C" al punto "H" y realiza cortes a la circunferencia con esa medida, situándote como punto de inicio el punto C.
6.- Une los puntos de corte de la circunferencia que realizaste anteriormente (#5).

Ejercicio 6.- Polígonos, Construcción de un cuadrado dentro de un circulo.
Los polígonos son figuras formadas por más de 3 lados los cuales forman su perímetro. Existen polígonos irregulares, los cuales son formados por lados de diferente longitud y los polígonos regulares, que son formados por los lados con la misma longitud.
Construcción de un cuadrado dentro de un circulo cualquiera.
1) Traza el diámetro y se traza una perpendicular, haciendo una mediatriz, se intersectan los arcos formados.
2) Los puntos formados en la circunferencia se unen, formando el cuadrado.

Los polígonos son figuras formadas por más de 3 lados los cuales forman su perímetro. Existen polígonos irregulares, los cuales son formados por lados de diferente longitud y los polígonos regulares, que son formados por los lados con la misma longitud.
Construcción de un cuadrado dentro de un circulo cualquiera.
1) Traza el diámetro y se traza una perpendicular, haciendo una mediatriz, se intersectan los arcos formados.

Ejercicio 5.- Desigualdad de los Triángulos.
Postulado de la desigualdad.
-En todo triángulo la suma de dos de sus lados cualquiera debe ser mayor a la medida del lado restante.
Determina si se pueden formar los triángulos con las siguientes medidas e indica que clase de triángulo es.
a) 4, 5 y 7
b) 6, 7 y 13
4+5= 9>7
5+7= 12>4
4+7= 11>5

Si se puede
6+7= 13=13
7+13= 20>6
6+13= 19>7
No se puede
Postulado de la desigualdad.
-En todo triángulo la suma de dos de sus lados cualquiera debe ser mayor a la medida del lado restante.
Determina si se pueden formar los triángulos con las siguientes medidas e indica que clase de triángulo es.
a) 4, 5 y 7
b) 6, 7 y 13
4+5= 9>7
5+7= 12>4
4+7= 11>5

Si se puede
6+7= 13=13
7+13= 20>6
6+13= 19>7
No se puede
Ejercicio 3.- Triángulos




MEDIATRIZ:
La mediatriz de un segmento es la recta perpendicular a dicho segmento trazada por su punto medio. Equivalentemente se puede definir como la recta cuyos puntos son equidistantes a los extremos del segmento. También se la llama simetral. Lugar geométrico de los puntos que equidistan de los extremos de un segmento AB.

BISECTRIZ:
La bisectriz de un ángulo es la semirrecta que pasa por el vértice del ángulo y lo divide en dos partes iguales. Es el lugar geométrico de los puntos del plano que equidistan (están a la misma distancia ) de las semirrectas de un ángulo.

ALTURA:
Es cada una de las rectas perpendiculares trazadas desde un vértice al lado opuesto (o prolongación). Se obtiene ortocentro que es el punto donde se cortan las 3 alturas).

MEDIANA:
Es cada una de las rectas que une el punto medio de un lado con el vértice opuesto. Se obtiene el baricentro que es el punto de corte de las tres medianas.

Clasificación de los Triángulos.
Según sus lados:
EQUILATERO: Cuando todos sus lados son iguales y también sus ángulos.
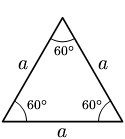 ISÓSCELES: Cuando dos lados son iguales y el tercero que es la base del triángulo es diferente.
ISÓSCELES: Cuando dos lados son iguales y el tercero que es la base del triángulo es diferente.

ESCALENO: Cuando todos sus lados son diferentes.




Según sus lados:
EQUILATERO: Cuando todos sus lados son iguales y también sus ángulos.


ESCALENO: Cuando todos sus lados son diferentes.
Según sus Ángulos:
ACUTÁNGULO: Cuando todos sus ángulos son agudos y miden 90°.

RECTÁNGULO: Cuando uno de sus ángulos es recto y es de 90°.

OBTUSÁNGULO: Cuando uno de sus ángulos es obtuso y mide 90°.
Fuentes:
Ejercicio 2.- Construcciones Básicas.
Ángulos Congruentes:
Un ángulo congruente es la unión de 2 rayos que tienen el mismo extremo u origen. Los ángulos se denominan por medio del símbolo y una letra griega o mayúscula.

Ángulos Congruentes:
Un ángulo congruente es la unión de 2 rayos que tienen el mismo extremo u origen. Los ángulos se denominan por medio del símbolo y una letra griega o mayúscula.

Construcción:
-Trazar un ángulo congruente:
1) Con el compás centrado en "A" (Osea el ángulo Original), trazas un arco con cualquier radio, tienes que cortar los dos rayos del ángulo, las intersecciones serán los puntos B y C.
2) Trazas un rayo con origen en "P".
3) Con la abertura que tenia el compás centra en "P" y traza un arco de circunferencia que cruce el rayo (Nombralo como Punto "Q")
4) Abre el compás con longitud ____ (Ángulo original)
BC
y centrado en Q, traza un arco de circunferencia que cruce el arco anterior (Nombralo como punto "R")
5) Traza el rayo uniendo los puntos "P" y "R".
Ejercicio 1.- ELEMENTOS GEOMÉTRICOS
Punto: Unidad más pequeña que se puede dibujar y se representa por una letra.
Punto: Unidad más pequeña que se puede dibujar y se representa por una letra.
.
A
Linea: Sucesión continua de puntos que se representa de la siguiente forma:
A. _____________ .B
____
AB
Plano: Sucesión continua de lineas:
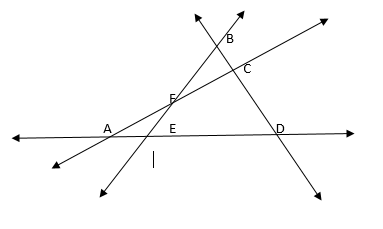
Puntos Colineales: Son aquellos que están sobre la misma recta.
Puntos no Colineales: Son aquellos que no están sobre la misma recta.

Grupos Colineales:
B, C, D. A, F, C. A, E, D.
Grupos no Colineales:
A, B, D. E, C, D. A, B, C. E, F, C. E, B, D.
Ángulos
Ángulo Agudo:
Un ángulo agudo es un ángulo que mide menos de 90°
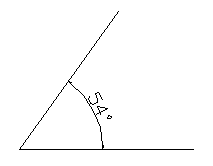

Este ángulo es agudo
Todos estos ángulos también son agudos:
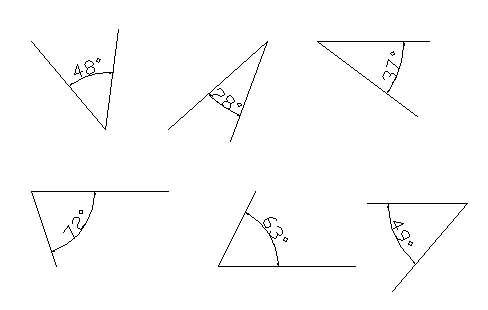
Acuérdate de fijarte en cuál de los dos ángulos es al que se refiere uno. Si el ángulo pequeño es menor que 90° entonces ese es agudo.
Ángulo Recto:
Un ángulo recto es aquel que mide 90°.

Ángulo Obtuso:
Un ángulo obtuso es un ángulo que mide más de 90° pero menos de 180°
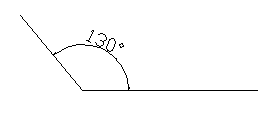 Todos estos ángulos también son obtusos:
Todos estos ángulos también son obtusos:
 Todos estos ángulos también son obtusos:
Todos estos ángulos también son obtusos: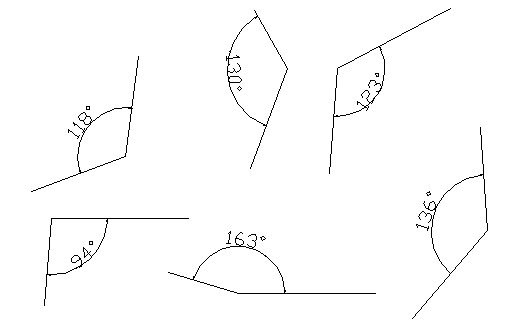
Ángulo Llano:
Un ángulo llano mide 180 grados
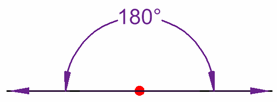
Ángulo Adyacente:
Son los ángulos formados por 2 ángulos consecutivos que tienen un vértice y un rayo en común, y juntos forman un ángulo llano.

Ángulos opuestos por el vértice:
Son los ángulos que, teniendo un vértice en común, los rayos de uno son prolongación del otro ángulo.

Ángulos Suplementarios:
Dos ángulos son suplementarios si suman 180 grados.

Ángulos Complementarios:
Dos ángulos son complementarios si suman 90 grados (un ángulo recto).
Fuentes:
http://es.wikipedia.org/wiki/%C3%81ngulo
Suscribirse a:
Comentarios (Atom)









